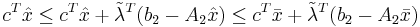Lagrangian relaxation
In the field of mathematical optimization, Lagrangian relaxation is a relaxation method which approximates a difficult problem of constrained optimization by a simpler problem. A solution to the relaxed problem is an approximate solution to the original problem, and provides useful information.
The method penalizes violations of inequality constraints using a Lagrangian multiplier, which imposes a cost on violations. When the Lagrangian multiplier is nonnegative and nonzero, some inequality constraint can be violated. In practice, the Lagrangian relaxed problem can be solved more easily than the original problem. The problem of maximizing the Lagrangian function of the dual variables (the Lagrangian multipliers) is the Lagrangian dual problem.
Contents |
Mathematical description
Given a linear programming problem 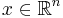 and
and 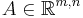 of the following form:
of the following form:
-
max 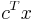
s.t. 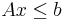
If we split the constraints in  such that
such that 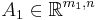 ,
, 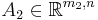 and
and 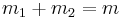 we may write the system:
we may write the system:
-
max 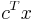
s.t. (1) 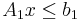
(2) 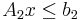
We may introduce the constraint (2) into the objective:
-
max 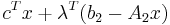
s.t. (1) 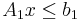
If we let 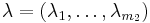 be nonnegative weights, we get penalized if we violate the constraint (2), and we are also rewarded if we satisfy the constraint strictly. The above system is called the Lagrangian Relaxation of our original problem.
be nonnegative weights, we get penalized if we violate the constraint (2), and we are also rewarded if we satisfy the constraint strictly. The above system is called the Lagrangian Relaxation of our original problem.
The LR solution as a bound
Of particular use is the property that for any fixed set of 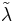 values, the optimal result to the Lagrangian Relaxation problem will be no smaller than the optimal result to the original problem. To see this, let
values, the optimal result to the Lagrangian Relaxation problem will be no smaller than the optimal result to the original problem. To see this, let 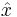 be the optimal solution to the original problem, and let
be the optimal solution to the original problem, and let 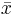 be the optimal solution to the Lagrangian Relaxation. We can then see that
be the optimal solution to the Lagrangian Relaxation. We can then see that
The first inequality is true because 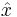 is feasible in the original problem and the second inequality is true because
is feasible in the original problem and the second inequality is true because 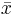 is the optimal solution to the Lagrangian Relaxation.
is the optimal solution to the Lagrangian Relaxation.
Iterating towards a solution of the original problem
The above inequality tells us that if we minimize the maximum value we obtain from the relaxed problem, we obtain a tighter limit on the objective value of our original problem. Thus we can address the original problem by instead exploring the partially dualized problem
-
min 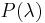
s.t. 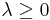
where we define 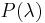 as
as
-
max 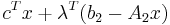
s.t. (1) 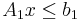
A Lagrangian Relaxation algorithm thus proceeds to explore the range of feasible  values while seeking to minimize the result returned by the inner
values while seeking to minimize the result returned by the inner  problem. Each value returned by
problem. Each value returned by  is a candidate upper bound to the problem, the smallest of which is kept as the best upper bound. If we additionally employ a heuristic, probably seeded by the
is a candidate upper bound to the problem, the smallest of which is kept as the best upper bound. If we additionally employ a heuristic, probably seeded by the 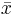 values returned by
values returned by  , to find feasible solutions to the original problem, then we can iterate until the best upper bound and the cost of the best feasible solution converge to a desired tolerance.
, to find feasible solutions to the original problem, then we can iterate until the best upper bound and the cost of the best feasible solution converge to a desired tolerance.
References
Books
- Ravindra K. Ahuja, Thomas L. Magnanti, and James B. Orlin (1993). Network Flows: Theory, Algorithms and Applications. Prentice Hall. ISBN 0-13-617549-X.
- Bertsekas, Dimitri P. (1999). Nonlinear Programming: 2nd Edition. Athena Scientific. ISBN 1-886529-00-0.
- Bonnans, J. Frédéric; Gilbert, J. Charles; Lemaréchal, Claude; Sagastizábal, Claudia A. (2006). Numerical optimization: Theoretical and practical aspects. Universitext (Second revised ed. of translation of 1997 French ed.). Berlin: Springer-Verlag. pp. xiv+490. doi:10.1007/978-3-540-35447-5. ISBN 3-540-35445-X. MR2265882. http://www.springer.com/mathematics/applications/book/978-3-540-35445-1.
- Hiriart-Urruty, Jean-Baptiste; Lemaréchal, Claude (1993). Convex analysis and minimization algorithms, Volume I: Fundamentals. Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences]. 305. Berlin: Springer-Verlag. pp. xviii+417. ISBN 3-540-56850-6.
- Hiriart-Urruty, Jean-Baptiste; Lemaréchal, Claude (1993). "14 Duality for Practitioners". Convex analysis and minimization algorithms, Volume II: Advanced theory and bundle methods. Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences]. 306. Berlin: Springer-Verlag. pp. xviii+346. ISBN 3-540-56852-2.
- Lasdon, Leon S. (2002). Optimization theory for large systems (reprint of the 1970 Macmillan ed.). Mineola, New York: Dover Publications, Inc.. pp. xiii+523. MR1888251.
- Lemaréchal, Claude (2001). "Lagrangian relaxation". In Michael Jünger and Denis Naddef. Computational combinatorial optimization: Papers from the Spring School held in Schloß Dagstuhl, May 15–19, 2000. Lecture Notes in Computer Science. 2241. Berlin: Springer-Verlag. pp. 112–156. doi:10.1007/3-540-45586-8_4. ISBN 3-540-42877-1. MR1900016.
- Minoux, M. (1986). Mathematical programming: Theory and algorithms (Translated by Steven Vajda from the (1983 Paris: Dunod) French ed.). Chichester: A Wiley-Interscience Publication. John Wiley & Sons, Ltd.. pp. xxviii+489. ISBN 0-471-90170-9. MR868279. (2008 Second ed., in French: Programmation mathématique: Théorie et algorithmes. Editions Tec & Doc, Paris, 2008. xxx+711 pp. ISBN-13: 978-2-7430-1000-3 MR2571910).
Articles
- Everett, Hugh, III (1963). "Generalized Lagrange multiplier method for solving problems of optimum allocation of resources". Operations Research 11 (3): 399–417. doi:10.1287/opre.11.3.39. JSTOR 168028. MR152360. http://or.journal.informs.org/cgi/reprint/11/3/399.
- Kiwiel, Krzysztof C.; Larsson, Torbjörn; Lindberg, P. O. (August 2007). "Lagrangian relaxation via ballstep subgradient methods". Mathematics of Operations Research 32 (3): 669–686. doi:10.1287/moor.1070.0261. MR2348241. http://mor.journal.informs.org/cgi/content/abstract/32/3/669.